[머신 러닝] Agglomerative(bottom-up) , top-down(divisive) - 컴도리돌이

Hierarchical clustering

 

 

->거리 행렬 사용한다.
->입력으로 clusters 수(=k)가 필요하지 않다. (input 값이 필요 없지만 알고리즘의 종료도 명확하지 않다.)
->언제 멈출지 결정해야 한다.
->bottom-up(agglomerative) and top-down(divisive) 접근

---

Agglomerative clustering(bottom-up)

 

1) single link clustering

->가장 가까운 인접 클러스터링
->두 그룹 G와 H 사이의 거리는 각 그룹의 가장 가까운 두 멤버 사이의 거리로 정의된다.

 

-Bottom-up approach example

Bottom-up approach example

1) 각 점과 점 사의 거리를 2 x 2 행렬로 표현한다.

 

2) 가장 가까운 점 두 개를 이어서 새로운 행렬을 다시 만든다.

 

d(1,2),3 = min(d1,3 , d2,3) = min (6,3) = 3

d(1,2),4 = min(d1,4 , d2,4) = min (10,9) = 9

d(1,2),5 = min(d1,5 , d2,5) = min (9,8) = 8

3) single link clustering example

2) complete linke clustering

->가장 먼 이웃 군집화
->두 그룹 G와 H 사이의 거리는 각 그룹의 가장 가까운 멤버 사이의 거리로 정의된다.

3) Average link clustering

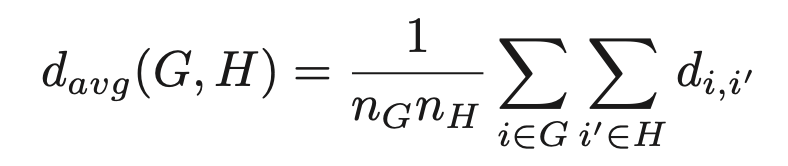
->모든 점 사이의 평균 거리 측정한다.

---

Divisive clustering

 

직경이 가장 큰 클러스터를 선택하고 K=2가 있는 k–means 알고리즘을 사용하여 분할

->한번 정해지면 그 안에서 cluster가 계속 반복된다.