outline
motivation
convolution operator(2 - dimention)
convolution operator(3 - dimention)
max/mean pooling operator
convolutional neural networks
structure of convolutional neural network
motivation
DNN은 기본적으로 1차원 형태의 데이터를 사용한다. 그렇기 때문에 이미지가 입력 값이 되는 경우, 이것을 flatten 시켜서 one hat-encoding으로 데이터로 만들어야 하는데 이 과정에서 이미지의 공간적/ 지역적 정보가 손실되게 된다. 추가로 추상화 과정 없이 바로 연산 과정으로 넘어가 버리기 때문에 학습시간과 능률의 효율성이 저하된다. 물론 학습은 시킬 수 있지만 overfitting isue가 존재한다. 이미지의 지역적 정보를 잘 살릴 수 있는 receptive field concept를 채용한 CNN이 도입되었다.
Convolution operator (2 - dimention)
5x5의 행렬로 표현된 이미지 입력 값이 있고 3x3 크기의 필터가 있다고 가정하자. convolution 연산은 입력값 이미지의 모든 영역에 같은 필터를 반복 적용해 패턴을 찾아 처리하는 것이 목적이다.
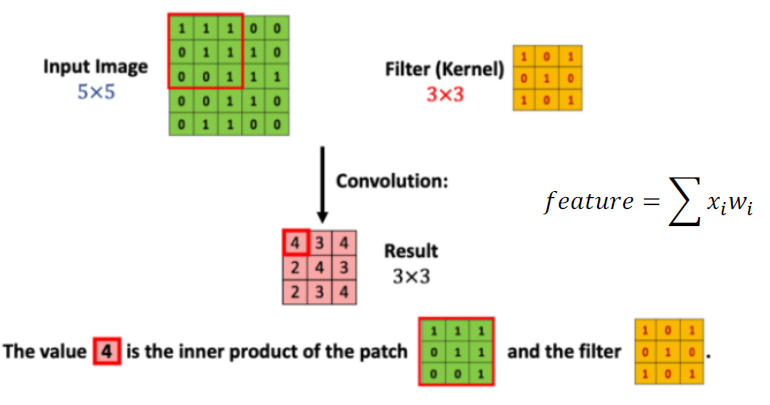
위의 그림을 예시로 보면 input image matrix의 빨간색 테두리 부분(3x3)과 filter matrix(3x3)를 inner product를 해준다. inner pruduct 연산을 해준 결과 값 4가 나온다. 4라는 값은 이미지의 필터 matrix가 갖고 있는 패턴이 얼마만큼 포함하는지 그 정도를 계산한 값이다.

- 첫 번째 연산을 마치고 필터를 한 칸 옆으로 옮겨주어서 다음 input image matrix의 빨간 테두리 영역과 filter matrix와 inner product 연산을 해주고 결과 값을 저장해준다.
- 이렇게 반복하여 얻어낸 결과 값이 Result matrix라고 분홍색(feature matrix)으로 표시된 matrix이다. filter matrix를 보면 해당 이미지가 'X' 형태의 패턴에 대해서 얼마만큼 갖고 있는지에 대해 정보를 갖고 있는 matrix이며 feature matrix라고도 부른다.
- 여기서 이상한 점은 input image는 5x5 행렬이지만 filter 처리를 마친 결과 값은 3x3행렬이 되었다. 이 얘기는 손실되는 부분이 발생한다는 뜻이다. 이러한 손실을 방지하기 위해 padding이라는 방법을 사용한다. 쉽게 말해 0으로 구성된 테두리를 이미지 가장자리에 감싸 준다고 생각하면 된다.
- Kernel Size : Kernel size는 convolution의 시야(view)를 결정한다. 보통 2d에서 3x3 픽셀로 사용된다.
- 이미지의 한 변의 크기를 n 필터의 한 변의 크기를 f라고 한다면, 결과 값의 크기는 (n-f+1) x (n-f+1)이다.
- ( 5 - 3 + 1) x ( 5 - 3 + 1) = 3 x 3
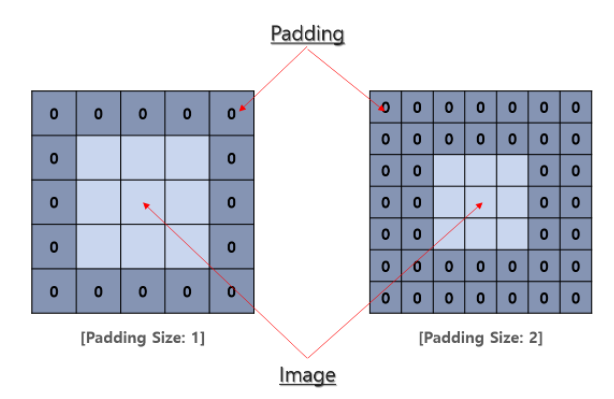
- padding : padding은 sample 테두리를 어떻게 조절할지를 결정한다. 패딩 된 convolution은 input과 동일한 output 차원을 유지하는 반면, 패딩 되지 않은 convolution은 커널이 1보다 큰 경우 테두리의 일부를 잘라버릴 수 있다.
- 입력된 데이터의 한 변의 크기가 n, 필터의 한 변의 크기가 f, 패딩의 양이 p라고 가정하자.
- 결과 값의 크기는 (n + 2p - f + 1) x (n + 2p - f + 1)이다.
만약 입력된 데이터의 크기와 결과 값의 크기를 같게 설정하고 싶으면 n + 2p - f + 1 = n의 수식을 만들 수 있으며, 결론적으로 패딩의 양을 p = (f - 1) /2로 설정하면 된다.

- stride : stride는 이미지를 횡단할 때 커널의 스텝 사이즈를 결정한다. 기본값은 1이지만 보통 max pooling과 비슷하게 이미지를 down sampling 하기 위해 stride를 2로 사용한다.
- 입력된 데이터의 한 변의 크기가 n, 필터의 한 변의 크기가 f, 패딩의 양이 p, stride 값을 s라고 가정하자.
- 결과 값의 크기는 ( (n + 2p - f) /2 +1 ) x ( (n + 2p - f) /2 +1 )이다.
convolution operator (3 - dimention)

입력 값이 3차원인 경우도 존재한다. 대표적인 예로는 컬러 이미지가 입력 값으로 들어왔을 경우인데, 컬러 이미지는 R, G, B의 세 가지 채널로 구성되어 있다. 그렇기 때문에 d1 x d2 x 3과 같은 삼차원의 크기를 갖는다. covolution 2- dimention과 동일하게 연산처리는 inner product를 사용한다. 여기서 주의해야 할 점은 이미지의 채널 수와 필터의 채널 수는 같아야 한다는 점이다. 하지만 출력 값의 채널 수는 같을 필요 없다.

위 그림은 zero padding이 된 R, G, B 입력 데이터가 들어왔고, 3개의 필터와 이미지를 down sampling을 하기 위해서 stride 값을 2로 설정하였다. 첫 번째 입력 값과 첫 번째 필터와 연산을 하게 되면 결과 값이 -1이 된다. 순차적으로 두 번째 세 번째의 연산 값은 2,1이 나왔다. 세 개의 결과 값과 bias를 합치면 결과 값은 최종적으로 3이 나오는 것을 확인할 수 있다.
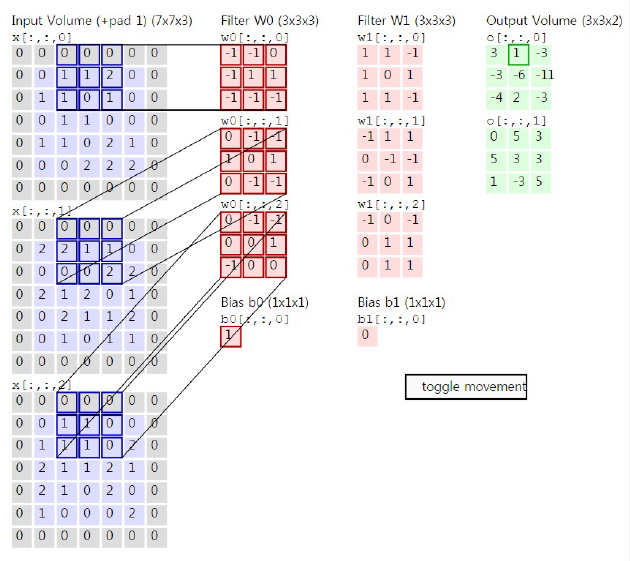
stride 값이 2이기 때문에 오른쪽으로 두 칸을 이동하여 동일한 convolution 연산을 하게 되면 0, 1, -1 값이 나오고 bias와 더해서 최종 결과 값이 1이 나오는 것을 확인할 수 있다.
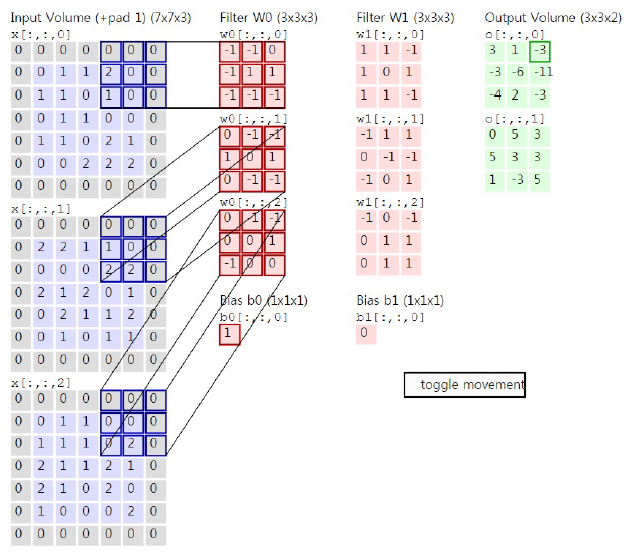
오른쪽으로 두 칸을 이용하고 필터와 convolution 연산을 하게 되면 결과 값이 -3,-2,0과 bias 값이랑 더하면 -4 값이 나오는 것을 확인할 수 있다.
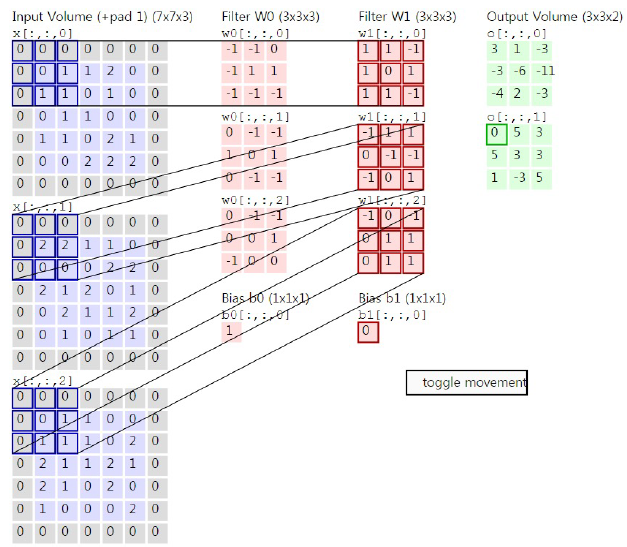
위의 예시에서는 결과 값을 두 개로 나오게 설정했기에 필터의 개수는 총 2개가 되어 동일한 연산으로 두 번째 결괏값을 도출한다.
- 입력으로 들어온 데이터의 한 변의 크기가 n, 채널의 수가 c, 필터의 한 변의 크기가 f , 필터의 수가 c` 가정하자.
- 입력 데이터의 크기 = n x n x c
- 필터의 크기 = f x f x c
- 결과 값의 크기 = ( (n + 2p - f) /2 +1 ) x ( (n + 2p - f) /2 +1 ) x c`
max/mean pooling operator
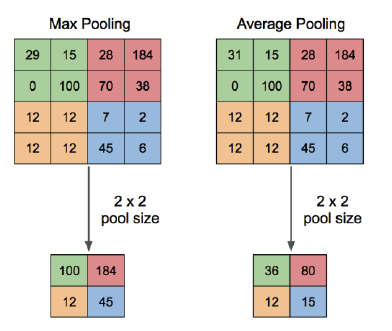
- max pooling : cnn에서 주로 사용하며, 해당 receptive field에서 가장 큰 값만 고른다.
- average pooling : recptive field 안에 존재하는 parameter 평균값을 갖고 온다.
- pooling을 사용하는 이유는 layer들을 거치고 나서 나온 ouput feature map의 모든 data가 필요하지 않기 때문이다. parameter를 줄이고, 해당 네트워크의 표현력이 줄어들어 ovefiiting을 억제하고 그만큼 비례하여 computation이 줄어들어 하드웨어 자원을 절약하고 연산 속도를 상승시킨다.
- pooling은 훈련을 통해 테스트되어야 할 parameter가 없으며, pooling의 결과는 채널 수에는 영향이 없으므로 채널 수는 유지된다. input feature map에 변화가 있어도 pooling의 결과는 변화가 적다.
- translation-invarient : 위치와 상관 없이 해당 정보가 있는지 없는지 확인할 수 있다.
CNN architecture
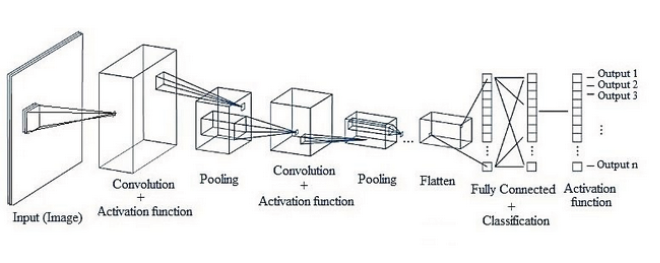
CNN의 구조는 기존의 fully-connected layer과는 다르게 구성되어 있다. cnn는 convolution layer과 pooling layer들을 활성화 함수 앞 뒤에 배치하여 만들어진다.
convolution layer
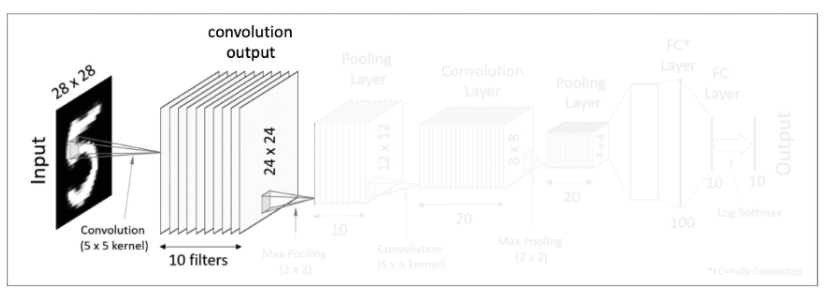
주어진 입력 값이 28x 28 크기를 가진 이미지라고 가정하면, 이 이미지를 대상으로 여러 개의 필터를 사용하여 결과 값을 얻는다. 한 개의 이미지 입력값에 10개의 5x5 필터를 사용하여 결과 값을 만들어 낸다. 그 후 도출해 낸 결괏값에 activiation fucntion을 적용한다.
pooling layer
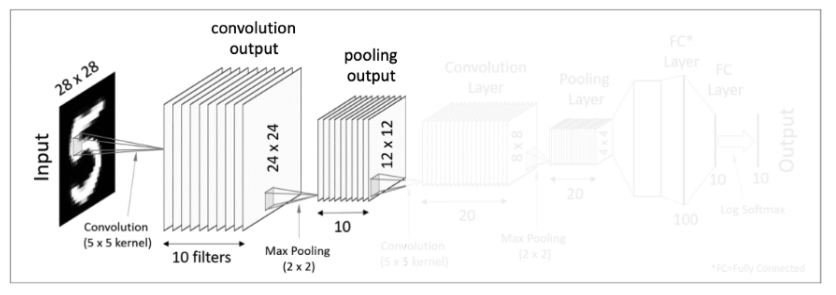
다음 pooling layer에서 2x2 max pooling을 하여 결과 값으로 10개의 12 x 12 matrics가 되었다.
mulitple convolutional layers
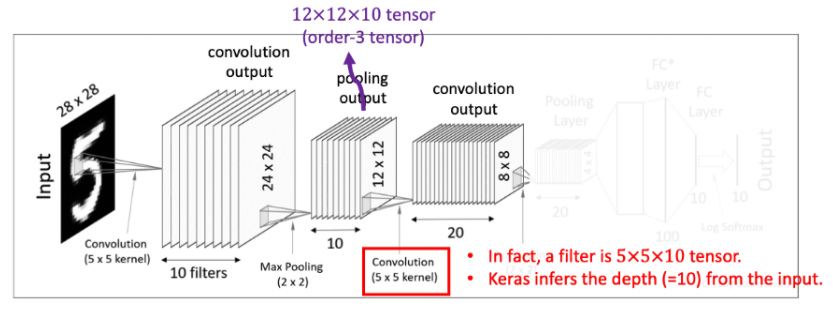
이번 convolution layer에서는 max pooling 연산을 마치고 나온 결과 값 12x12x10차원을 대상으로 5x5x10 크기의 필터를 20개를 사용해준다. 그러면 8x8 크기를 가진 결과 값을 20개를 얻어 낼 수 있다.
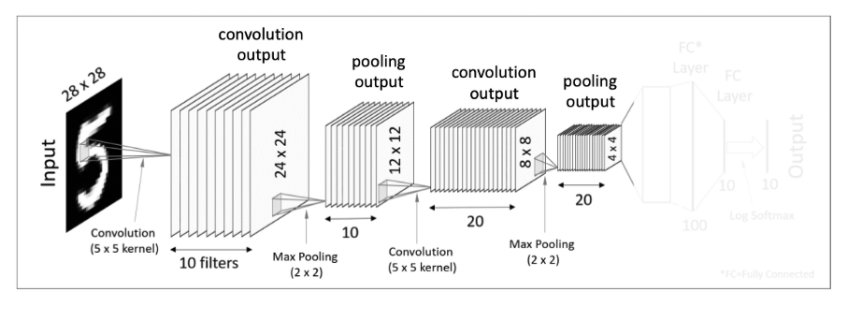
두 번째 max pooling 연산을 하여 결과 값으로 20개의 4x4 matrics를 얻어낸다.
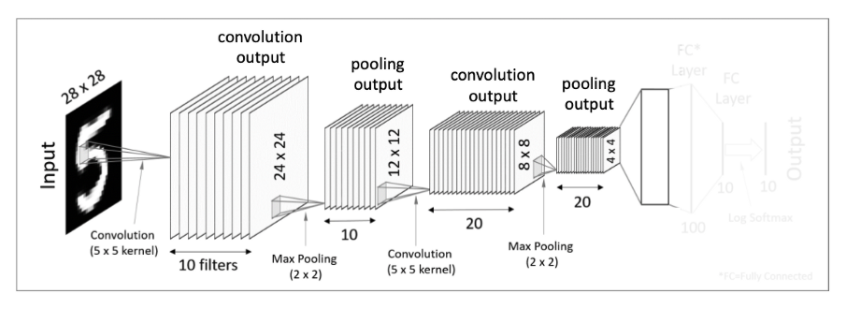
그 후 4x4x20 matrics를 flatten을 시켜준다. flatten을 시켜 준다는 개념은 다차원 데이터들을 1차원 데이터로 바꾼다는 생각 하면 된다.
final layer - Fully-Connected layer
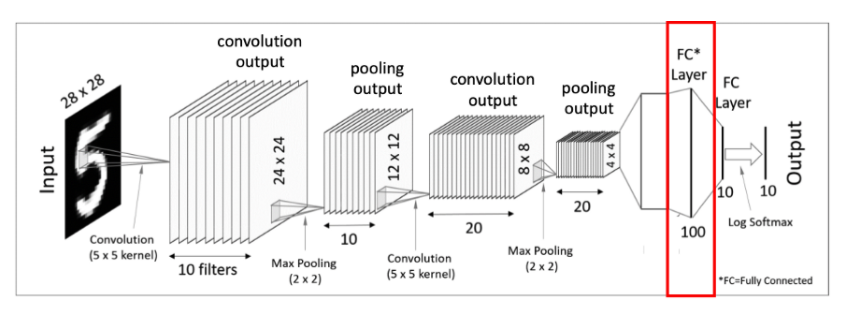
마지막으로 fully-connected layer를 적용시키고 softmax activation function을 적용해주면 결과 값을 출력하게 된다.
the number of total wegiht parameters
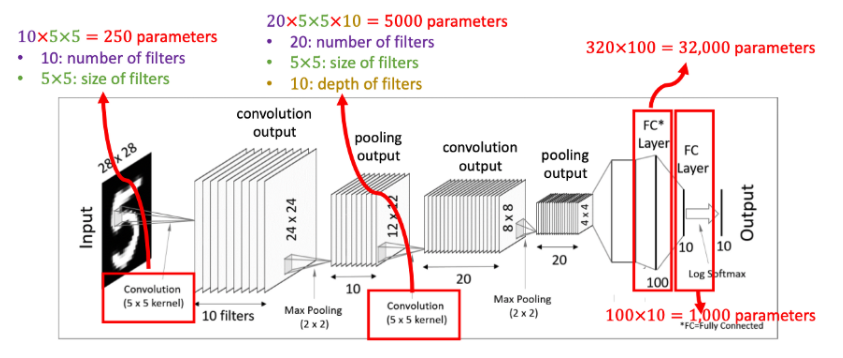
- 첫 번째 convolution layer에서 5x5 크기의 필터 10개를 사용했기 때문에 250개의 매개변수가 존재한다.
- 두 번째 convolution layer에서는 5x5x10 크기의 차원을 20개의 필터를 사용했기 때문에 5000개의 매개변수가 존재한다.
- 첫 번째의 fully-connected layer에서 pooling output의 4x4x20에서 100개의 weight를 연산했기에 32000개의 매개 변수가 존재한다. 해당 fully-connected layer을 사용하는 이유는 결과적으로 해당 입력 데이터를 예측하기 위해서 output을 만들어야 하는데 output 연산을 조금 더 쉽게 처리하기 위해서 만들어둔 장치라 생각하면 된다.
- 두 번째 fully-connected layer에서는 100개의 결과물에서 10개의 weight를 연산했기에 1000개의 매개 변수가 존재한다.

